日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾　Vol.11

（１）
ヒント②の通り、「３で割り切れる」とは、その数が「３の倍数」だということですから、まずは１～100の数の中に「３の倍数」がいくつあるか数えてみましょう。１から100までの中にある３で割れる数（３の倍数）は下記のように求められます。
　（ア） ３の倍数：100÷３＝33あまり１　➡︎33個

この計算結果を見て、「３で割れなくなるのは34回目だ！」と答えたくなりますが、実はこれだと間違いです。それはなぜでしょうか？
例えば「９」は３で２回割れますし、ほかにも「18」や「36」も２回割れます。そして、３で２回割れる数とは、言い換えれば「９の倍数」のことです。
では、９の倍数は１から100までの中に何個あるでしょうか?３の倍数の個数を数えるときと考え方は同じです。
　（イ） ９の倍数：100÷９＝11あまり１　➡11個
３で２回割れる数が11個あるとわかりました。３の倍数でカウントしたぶんの重複は除くので、11個を加算します。

さて、これで終わりではありません。３回割れる数はないでしょうか？それは、３×３×３＝27です。つまり27の倍数は、３で３回も割れることになります。
　（ウ） 27の倍数：100÷27＝３あまり19　➡３個
３で３回割れる数が３個あるとわかりました。３の倍数・９の倍数でカウントしたぶんの重複は除くので、３個を加算します。

あともう一息！今度は３で４回割れる数、３×３×３×３＝81です。この数は、さらにもう１回、３で割ることができます。
　（エ） 81の倍数：100÷81＝１あまり19　➡１回
３で４回割れる数が１個あるとわかりました。３の倍数・９の倍数・27の倍数でカウントしたぶんの重複は除くので、１個を加算します。

100以下には３で５回以上割れる数はありませんので、これでおしまいです。

以上より、１から100までの数の中には、３で１回だけ割れる数が33個、ちょうど２回割れる数が11個、ちょうど３回割れる数が３個、ちょうど４回割れる数が１個あることがわかりました。これらをすべて足した数が、Nを３で割れる回数になります。つまり、33＋11＋３＋１＝48です。よって３で割り切れなくなるのは、49回目となります！（解説１）

（２）
次は、Nを42で何回割れるかを考えます。数が大きくなったので戸惑うかもしれません。
ヒント③でも触れた通り、42は42＝２×３×７と分解できますので、「42で１回割る」とは、「２と３と７でそれぞれ１回ずつ割る」のと同じ操作です。つまり、２と３と７それぞれで何回割れるかを別々に考えていけば理解しやすくなります。

Nを２で割れる回数と、３で割れる回数と、７で割れる回数の中で一番数が多くなるのは、２の倍数ですね。逆に、割れる回数が一番少ないのは７の倍数です。
また、「２と３と７でそれぞれ１回ずつ割る」ためには、因数に２と３と７がセットで必要です。割れる回数が一番少ないのは７なので、Nが７で何回割れるかを考えればOKです。それがそのまま答えになります。（解説２）

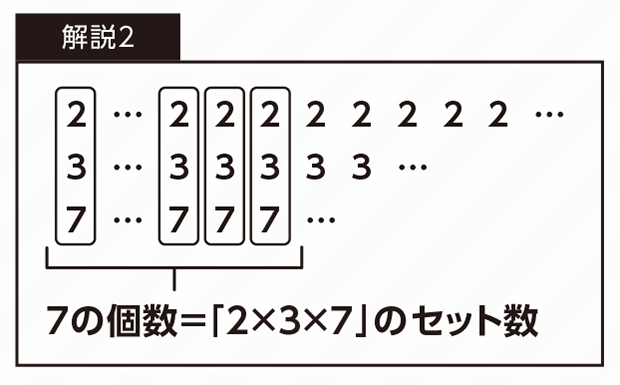
あとは⑴の解き方を思い出して計算してみましょう。
　・７の倍数：100÷７＝14あまり２　➡14個
　・49の倍数：100÷49＝２あまり２　➡２個
14＋２＝16回ですから、割り切れなくなる回数は17回目とわかります。これが求める答えですね!