日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾　Vol.10

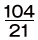　「と 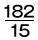、それぞれとの積がどちらも自然数となるような分数のうち、最も小さいもの」を答える問題です。【ヒント①】で触れたとおり、求めたい分数の分子と分母を別々に考えるとよいでしょう。（ここでは仮に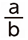としておきます。）【ヒント③】の通り、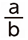を最も小さくするためには、その分子aはできるだけ小さく、分母bはできるだけ大きいものを探しましょう。
　では、その分子aと分母bについて、それぞれ考えていきます。

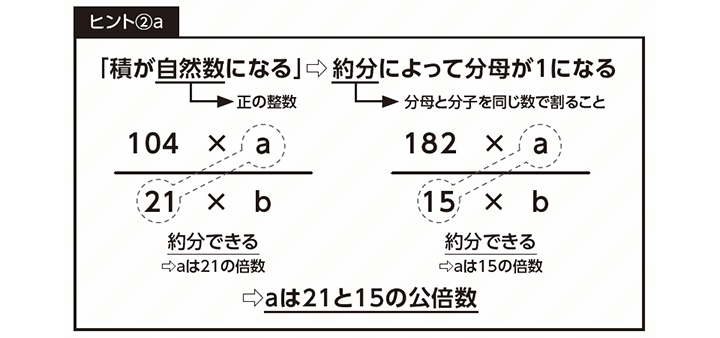
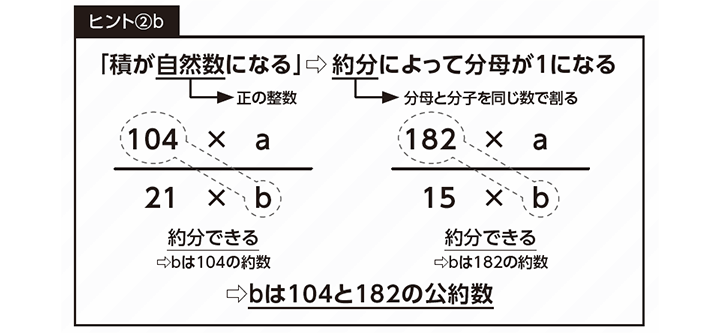
　まずは分子aを考えます。【ヒント②】で触れた通り、「 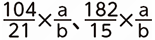がどちらも自然数（正の整数）となる」ということは、分母である21、15、bは約分（分母と分子を同じ数で割る）によって消せる（分母が1になる）ということです。つまり求める分数の分子aは、21と15の両方で割り切れる正の整数だとわかります。
　「21で割れる数」とは、21にある自然数をかけた数、すなわち「21の倍数」です。具体的には、21,42,63,…などですね。
　同様に、「15で割れる数」とは、「15の倍数」（15,30,45,…）のことです。
　この両方を満たす必要があるので、求める分数の分子aは、「15の倍数」でもあり「21の倍数」でもある数（これを「15と21の公倍数」と言います）が当てはまります。

　さらに、【ヒント③】の通り、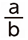を最も小さくするためには、その分子aはできるだけ小さくする必要があります。すなわち、15と21の公倍数のうち最も小さい数（これを「15の21の最小公倍数」と言います）を求めればいいですね。
　21の倍数は小さいものから順に21,42,63,84,105,126,…となります。一方15の倍数は小さいものから順に、15,30,45,60,75,90,105,120,…です。21と15の公倍数のうち最も小さい数（21と15の最小公倍数）は、105とわかりました！

　続いて分母bを考えましょう。【ヒント②】で触れた通り、「 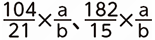がどちらも自然数（正の整数）となる」ということは、分母である21、15、bは約分（分母と分子を同じ数で割ること）によって消せる（分母が1になる）ということです。つまり求める分数の分母bは、104と182の両方を割り切ることができる正の整数でないといけないことがわかります。
　「104を割り切れる数」とは言い換えれば、「104の約数」です。約数とは「ある整数に対して、その数を割り切ることのできる整数」のことで、例えば12なら1,2,3,4,6,12が挙げられますが、これらはすべて12の約数です。
　つまり、分母ｂは、「104の約数」でも「182の約数」でもある数（これを「104と182の公約数」と言います）が当てはまります。

　さらに、【ヒント３】の通り、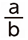を最も小さくするためには、その分母bはできるだけ大きくする必要があります。つまり、この分母ｂは104と182の公約数の中で最も大きい数（これを「104と182の最大公約数」と言います）ということです。
　104の約数は、1,2,4,8,13,26,52,104。一方182の約数は、1,2,7,13,14,26,91,182です。ここから、104の182の公約数のうち最も大きい数、すなわち104と182の最大公約数は26であることがわかります。

　以上より、求めたい分数の分子aが105、分母bが26とわかりましたので、答えはですね！