日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾 Vol.9

Point-考え方-
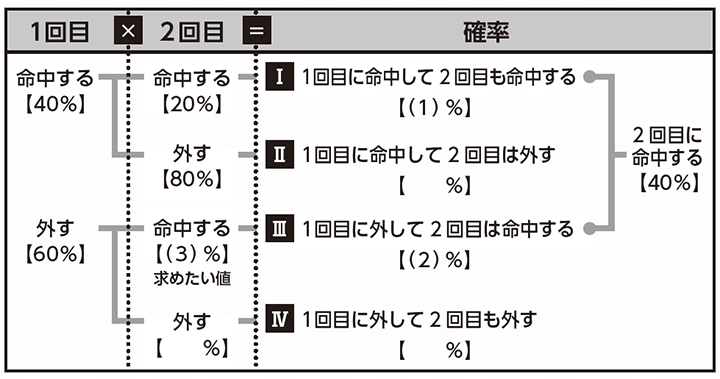
この的あてゲームでは、1回目と2回目のそれぞれで命中するかどうかによって、結果を4つのパターン(Ⅰ~Ⅳ)に分けることができます。ヒント①の通り、樹形図に書き出し、さらにヒント②~④を参考に、問題文中で判明している確率の値を書き入れてみましょう【下図】。
ではまずは、どのような順序で解いていくかを検討しましょう。
今回求めたい値である「1回目に外した場合の2回目の命中率」は、図右の⑶です。
ヒント③の通り、⑵「1回目に外して2回目は命中する確率」とは区別してくださいね。
ヒント④で示した通り、⑵「1回目に外して2回目は命中する確率」は、「1回目に外す確率」と⑶「1回目に外した場合の2回目の命中率」の積(掛け算)で求められます。よって、「1回目に外す確率」が60%とわかっていますので、⑵がわかれば⑶は求められます。
そして、ヒント②の通り、「2回目の命中率」は⑴「1回目に命中して2回目にも命中する確率」と⑵「1回目に外して2回目は命中する確率」の和(足し算)ですね。ⅠとⅢの確率の和(⑴+⑵)が40%とわかっていますから、⑴の値がわかれば⑵も求められます。
⑴はヒント④の通り「1回目の命中率」と「1回目に命中した場合の2回目の命中率」の積(掛け算)で求められますから、すでに材料はそろっています。
よって、⑴→⑵→⑶の順番で計算していきましょう!
解く順序が決まったところで、実際に計算していきます。
⑴はヒント④の通り、「1回目の命中率」と「1回目に命中した場合の2回目の命中率」の積(掛け算)で求められます。
40%(0.4)×20%(0.2)=8%(0.08) …⑴
次に、先ほど求めた⑴を使って、⑵を計算しましょう。
40% (0.4)-8%(0.08)=32%(0.32) …⑵
最後に、先ほど求めた⑵を使って⑶を計算しましょう。
60%(0.6)×⑶=32%(0.32)の方程式を解きます。
32%(0.32)÷60%(0.6)≒53%(0.53) …⑶
これで求めたい値が計算できました!約53.3%(分数で表すと8/15)が答えですね!
Answer
2022年6月号でも紹介しましたが、「条件Aを満たす場合のもとで条件Bも満たす確率」を「条件付き確率」と言います。例えば、迷惑メールのフィルタリングには、「リンクが貼ってあるか」「特定の言葉(例:『援助』『出会い』など)が使われているか」などの条件をもとに、迷惑メールである確率を推定する方法(ベイズ推定)が用いられています。条件付き確率を理解することで、日常やビジネスシーンでも一見「ややこしい」問題をスムーズにひも解けるようになっていくはずです!ぜひがんばって習得してみてくださいね。
条件付き確率のエッセンスを感じていただけたでしょうか?
次回は12月号(11/1発刊)に掲載予定です。お楽しみに!
[『TACNEWS』 2022年10月号|連載|ティーチャー鈴木の数的センスアップ塾]
筆者 鈴木 伸介(すずき しんすけ)
TAC統計検定®・ビジネス数学検定 ・中小企業診断士講座講師
株式会社数学アカデミー代表取締役
各種数学セミナーで講師活動を行いながら、社会人向け数学教室「おとなのENJOY!数学クラブ」「おとな数学オンライン」を主宰、ビジネスパーソンの数学リテラシー向上に尽力している。
保有資格:中小企業診断士・統計調査士・ ビジネス数学検定1級AAA
著 書 : 『もう一度解いてみる入試数学』(すばる舎)
















