日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾　Vol.8

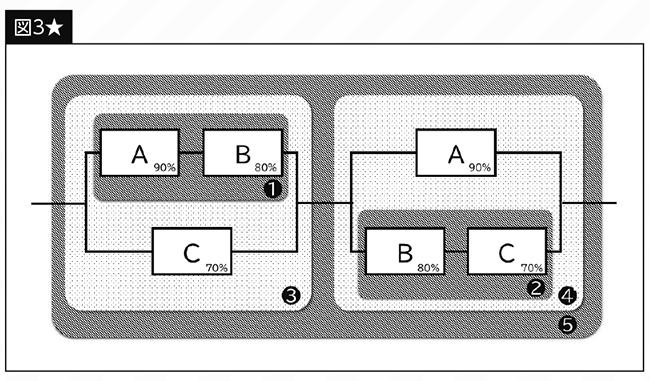
まず【図３】から検討していきましょう。これは上の【図3★】のように分解することができます。❶～❺の順に正常に動く確率を計算していきましょう。

❶は「AとBの直列接続」、❷は「ＢとＣの直列接続」ですから、【図１】の計算で求められます。
❶…0.9×0.8＝0.72
❷…0.8×0.7＝0.56
続いて❸ですが、これはＡとＢをひとつのカタマリとみなすことで、「❶とＣの並列接続」と考えることができます。
❹も同様に「Ａと❷の並列接続」と考えられますね。【 図２】の計算で求めてみましょう。
　❸…１-{（１-0.72）×（１-0.7）}=１-（0.28×0.3）＝0.916
　❹…１-{（１-0.9）×（１-0.56）}=１-（0.1×0.44）＝0.956
最後に❺です。これは「❸と❹の直列接続」と考えられますね！
　❺…0.916×0.956＝0.875696　＜約87.6％＞

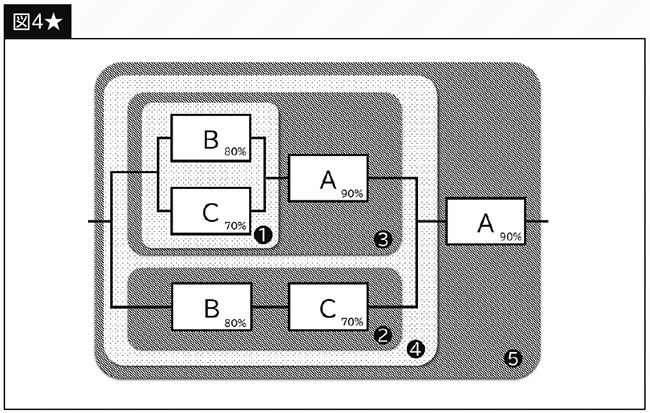
同じ要領で今度は【図４】に挑戦してみましょう。これは右の【図4★】のように分解できます。
❶は「ＢとＣの並列接続」、❷は「BとCの直列接続」ですね。
　❶…１-{（１-0.8）×（１-0.7）}=１-（0.2×0.3）＝0.94
　❷…0.8×.0.7＝0.56
❸は「❶とＡの直列接続」です。
　❸…0.94×0.9＝0.846
❹は「❷と❸の並列接続」です。
　❹…１-{（１-0.56）×（１-0.846）}=１-（0.44×0.154）＝0.93224
❺は「❹とAの直列接続」です。
　❺…0.93224×0.9＝0.839016　＜約83.9％＞
以上より、全体が正常に作動する確率は、【図３】が約87.6％、【図４】が約83.9％なので、答えは【図３】ですね！