日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾 Vol.7

Point-考え方-
本問のような数学のジャンルを「集合論」といいます。ある条件を満たすものの集まりを「集合」として、ベン図を使って分析するのが一般的です。これによって、ある条件を満たすものの個数を計算処理できるほか、論理の分析にも応用できます。
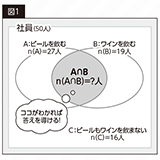
さてこの問題では、全社員が50人、「A.ビールを飲む」人が27人、「B.ワインを飲む」人が19人、「C.ビールもワインも飲まない」人が16人と与えられていますので、まずはこの情報をベン図に書き込んでみましょう。
また、今回求めたいのは、「この部署の中から選んだひとりの社員が『A.ビールを飲む』と答えていた場合に、この人が『B.ワインを飲む』とも答えている確率」です。この確率を求めるには、ヒント①の通り、分子となる「ビールとワイン両方を飲む」人の人数と、分母となる「ビールを飲む」人の人数が必要ですね。後者はすでに問題で27人と提示されているのでOK。したがって、前者の「ビールとワイン両方を飲む」人の人数、つまりヒント②で示したベン図でいうと、「A.ビールを飲む」と「B.ワインを飲む」の円の重なる部分に含まれる人数がわかれば答えを導けるということです。
<数学知識をプラス!>
・「AかつB」を「A∩B」(AキャップB)、「AまたはB」を「A∪B」(AカップB)と表します。
・「A」や「A∩B」などに含まれる個数を、それぞれ「n(A)」「n(A∩B)」という風に「n」を使って表します。
「n(A∩B)」を求めるためには、手元にある情報をどう組み合わせればいいのか…。解説を読み進める前にぜひベン図を見ながら解き方を考えてみてください。【図1】
さて、今回の問題では2通りのアプローチを取ることができますが、どちらのアプローチもまず「n(A∪B)」の数が必要になります。
「n(A∪B)」は下記のように求められます。【図2】
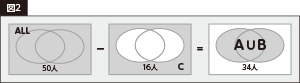
数字を当てはめると、n(A∪B)は50-16=34だとわかります。
では、ここからはアプローチ別に見ていきましょう。
1つ目は、「ビール(ワイン)を飲む人」と「ビール(ワイン)は飲むけどワイン(ビール)は飲まない人」(三日月形の部分)の人数との差から求める方法です。【図3】
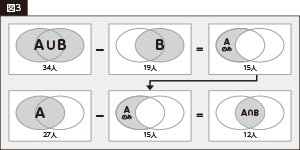
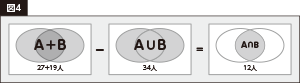
そして2つ目は、n(A)+n(B)と n(A∪B)の差から求める方法です。【図4】
どちらの方法でも「n(A∩B)」は12人と求めることができます。
これで必要な数字が揃いました。
求めた数を条件付き確率の式に当てはめると、「ビールとワイン両方を飲む」人の人数/「ビールを飲む」人の人数 = 12/27 = 4/9とわかります。
これが答えですね!
Answer
「条件付き確率」は紹介した記号を使うと、n(A∩B)/n(A)と表せます。一般的には、P(A∩B)/P(A)と書かれていることが多いですが、これは「個数(n)」を「確率(P)」(確率Probabilityの頭文字)に変えただけで、本質的な考え方は同じです。ベン図や条件付き確率、ここから発展する“ベイズの定理”は、現代統計学の基礎として、例えば迷惑メールのフィルタリングなど日常生活にかかわる部分でも活用されています。
ぜひこういった身近な例から数学への興味を深めてくださいね。
ベン図をマスターしてビジネスにも活用してみてくださいね!
次回は8月号(7/1発刊)掲載予定です。お楽しみに!
[『TACNEWS』 2022年6月号|連載|ティーチャー鈴木の数的センスアップ塾]
筆者 鈴木 伸介(すずき しんすけ)
TAC統計検定®・ビジネス数学検定・中小企業診断士講座講師
株式会社数学アカデミー代表取締役
各種数学セミナーで講師活動を行いながら、社会人向け数学教室「おとなのENJOY!数学クラブ」「おとな数学オンラインサロン」を主宰、ビジネスパーソンの数学リテラシー向上に尽力している。
保有資格:中小企業診断士・統計調査士・ ビジネス数学検定1級AAA
著書 : 『もう一度解いてみる入試数学』(すばる舎)
















